Il flusso di un gas o di un liquido viene misurato per diverse ragioni, incluse sicuramente anche le considerazioni commerciali come ad esempio la parte di un contratto o nei processi produttivi. Il flusso o portata (volume/tempo) può essere rilevato, tra gli altri metodi, tramite la pressione.
La portata può essere misurata in vari modi. Oltre ai sensori di flusso ad ultrasuoni e ai sensori di flusso magnetico-induttivi, esistono anche sensori che funzionano in base al processo di pressione differenziale, tra cui rientrano il diaframma con orifizio calibrato, il tubo Venturi e il tubo di Pilot-Prandtl. Per valutare i valori misurati, con tutti i sensori che funzionano secondo il processo di pressione differenziale si utilizza l’equazione di Bernoulli:
Q = V/t = VmA
Q = portata
Vm = velocità media
t = tempo
A = area
V = volume
Prendiamo come esempio la misurazione della portata volumetrica tramite diaframma calibrato. Attaccando il diaframma al tubo, quest’ultimo si restringe in un punto:
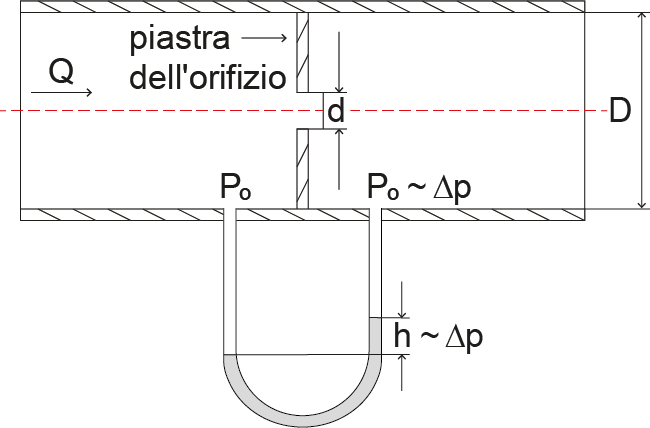
Immagine 1: Misurazione del flusso tramite diaframma
In caso di flusso regolare, deve verificarsi la stessa pressione prima e dopo l’orifizio:
p1 + ½ ρv12=p2+ ½ ρv22
p = pressione
ρ = densità
v = velocità
Questo assunto si basa sull’equazione di continuità che afferma che tutto ciò che scorre in un tubo alla fine fuoriesce:
v1A1 = v2A2
v = velocità
A = area

Immagine 2: misurazione del flusso
In condizioni reali, però, si genera un attrito che causa una caduta di pressione:
p + ½ ρv2 + wR = costante
P= pressione
ρ = densità
v = velocità
wR = forza di attrito per volume

Immagine 3: caduta di pressione dovuta all’attrito
La caduta di pressione è importante per determinare la portata volumetrica. Tuttavia, l’effetto di attrito dipende da molti fattori. Per questo motivo si utilizza una formula empirica basata a sua volta su valori empirici. La pressione volumetrica deriva, infine, dalla radice della pressione differenziale:
Q = 4000 αεd2√∆p/ρ
Q = portata volumetrica
α = coefficiente di flusso empirico
ε = fattore di espansione
d = diametro interno dell‘orifizio
∆p = pressione differenziale
ρ = densità
Per rendere questa formula un po’ più semplice per gli utenti, tutti i valori costanti dello strumento di misura e del fluido di misura vengono riassunti come costante “c”. Da ciò deriva, ad esempio per un fluido, la seguente equazione:
Q = c √∆p
